大家好，我是小麦。

以前做控制相关的项目，总会遇到PID的算法，在工程领域，这无疑是简单，实用，有效的一个算法。

只需要调整比例，积分，微分的参数，就能达到比较好的控制效果。

但是这其中，我们最好是知其然，知其所以然。

控制其实是一门比较综合的学科，有时候感觉它是批着控制外衣的数学，下面是国外大佬Brian Douglas总结的图解控制理论，如下图所示；

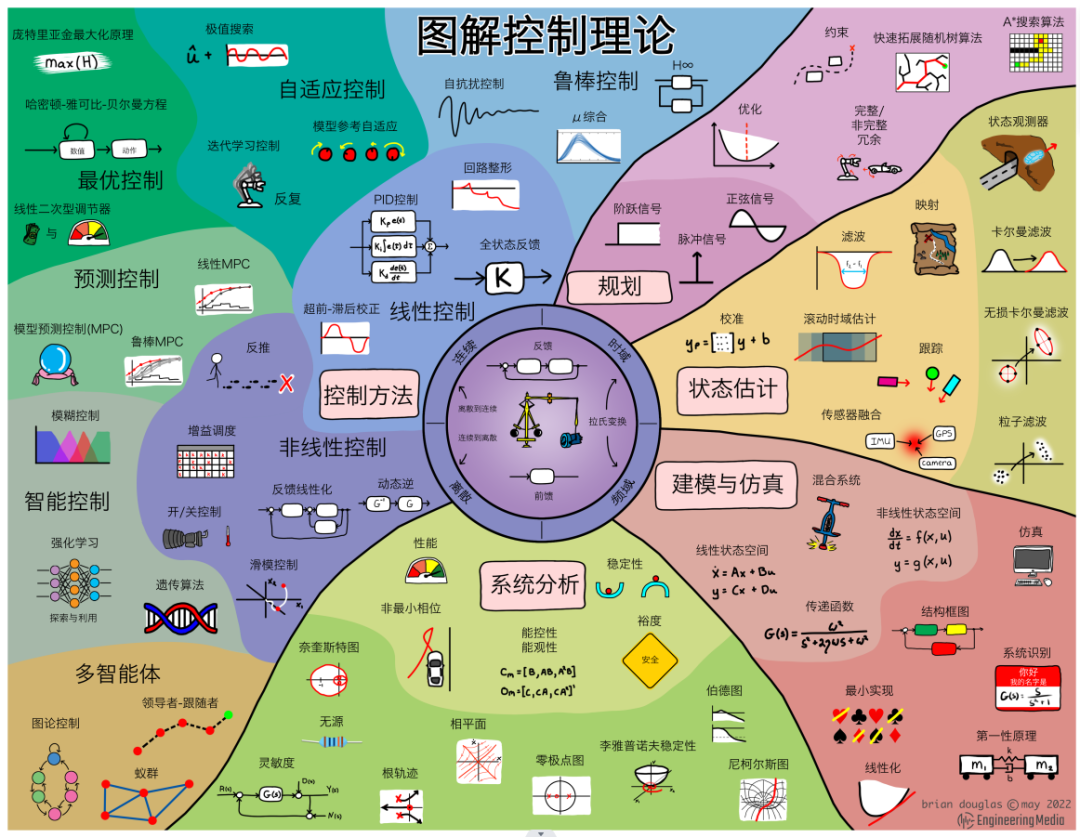
From Brian Douglas

控制理论是庞然大物，后来我在B站看到DR_CAN的视频，中文讲解，由浅入深，受益匪浅。

所以这里给大家强烈安利DR_CAN的新书《控制之美（卷1）——控制理论从传递函数到状态空间》，配合视频看，效果不错。老规矩，文末送书

解决一个控制系统的问题，可以分为三个步骤。

第一步需要对所研究的对象进行系统分析，建立数学模型，有可能是热力学，动力学，流体，甚至是生态或者经济学模型。

第二步是在这个数学模型的基础上进行控制器的设计。可以应用到不同的控制手段和方法。

最后一步就是测试。

这里面需要有测试模型的搭建，实验设计，当然还会涉及到一些数据处理。

同时实验设备在做出来之后，也需要把实验结果与建模进行比较，对数学模型进行验证和不断地更新。

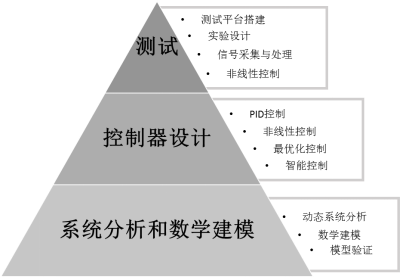
如图所示，动态系统的分析和数学建模是分析控制系统的基础，后续的工作都将在这一个基础上完成。

在这里我们用两种不同的方法介绍动态系统的分析与数学建模。

首先重点讨论经典控制理论的建模方法，即采用拉普拉斯变换和传递函数的办法来描述系统。

从动态系统的本质入手，重点解释如下三个问题：

• 动态系统的本质是什么？

• 为什么在经典控制中引入拉普拉斯变换，意义和好处在哪？

• 传递函数的涵义和控制系统设计的基本概念。

对于动态系统来说，系统状态变量会随着时间变化。

对动态系统进行数学建模就是用等式去描述系统状态变量的变化规律。

本文中，如果不另外说明，研究的对象是线性常系数微分方程，对应的系统就是线性时不变系统

从严格意义上来讲，时不变系统是不存在的，因为“人不能两次踏进同一条河流”，而在大部分工程情况下，可以把问题近似简化为时不变系统。

就是说在系统分析的时间区间内，系统的参数是恒定的。对于非线性的系统，一般可以在系统的平衡点附近做线性化处理。不可以近似为线性时不变的系统不在本书的讨论范围之内。

对于一个线性时不变系统而言，可以通过一个冲激响应得到系统的全部特性。而系统的输入与输出是卷积的关系。用简单直观的语言来说就是系统的输入会对未来一段时间之内的系统输出产生影响。

可以做一个简单的比喻；

• 向水中扔一枚石子，会产生涟漪。

• 如果在第一次涟漪消失之前，又向水中扔了另一颗石子，那么这两次的涟漪就会叠加。

• 这其中，扔石子这个动作就是系统的输入，水面就是系统本身，而产生的涟漪就是系统的输出。

这说明，某一个时刻的涟漪，是前面几次石子入水后的叠加的效果。

这个叠加用数学语言来表示就是卷积，下面通过一个例子来推导一下卷积的公式，一步步揭开卷积的面纱，从而了解动态系统的本质。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。